Skip to main content

🔍 Comparators and Signal Conditioning

So far, we’ve learned how to amplify signals. Now we move to the next critical step in real-world electronics:
👉 deciding (yes/no) and preparing signals so digital systems can understand them.

This is where comparators and signal conditioning come in.

⚖️ Comparators – The Yes/No Decision Maker​

A comparator answers a simple question:

“Is this voltage higher than that voltage?”

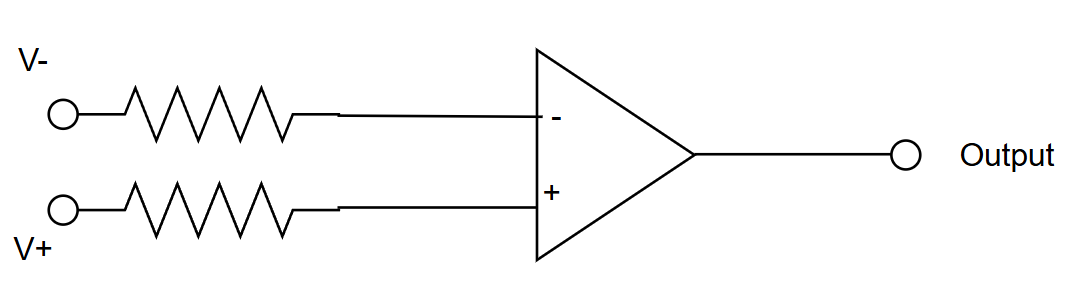
How a Comparator Works​

  • Voltage at non-inverting (+) input
  • Voltage at inverting (−) input

Behavior:

  • If V+>V−V_+ > V_- → Output goes HIGH
  • If V+<V−V_+ < V_- → Output goes LOW

There is no feedback.
The op-amp is used in open-loop mode, so even tiny differences force the output to saturate.

🧪 Practical Comparator Example​

Temperature sensor:

  • 0∘C→0V0^\circ C \rightarrow 0V
  • 10mV/∘C10mV / ^\circ C

Threshold: 30∘C⇒300mV30^\circ C \Rightarrow 300mV

Comparator Setup​

  • Sensor → V+V_+
  • Reference 300mV300mV → V−V_-

Result:

  • Temperature < 30∘C30^\circ C → Output LOW
  • Temperature > 30∘C30^\circ C → Output HIGH (alarm ON)

Simple. Effective.

⚠️ Comparator Problem: Noise & Chatter​

Near the threshold:

  • Noise
  • Ripple
  • Sensor instability

This causes the output to rapidly toggle: HIGH → LOW → HIGH → LOW

This is chattering, and it’s bad for:

  • Relays
  • Digital inputs
  • Microcontrollers

🔁 Hysteresis – The Stability Fix​

Hysteresis adds two thresholds:

  • One for turning ON
  • One for turning OFF

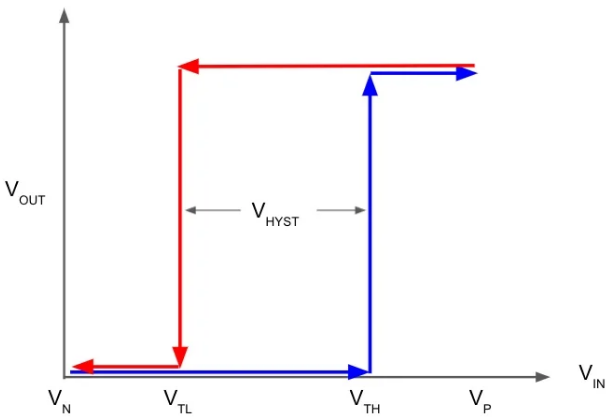
In the graph VTLV_{TL} is lower threshold and VTHV_{TH} is upper threshold

Hysteresis is introduced using positive feedback, creating two different switching thresholds:

  • Upper Threshold (VTHV_{TH})

  • Lower Threshold (VTLV_{TL})

This prevents noise from causing multiple output transitions near the threshold.

Just like a thermostat.

Example​

  • Turns ON at 300mV300mV
  • Turns OFF at 280mV280mV

Noise between 280–300mV280–300mV no longer matters.

Inverting Comparator with Hysteresis​

note

The input signal is applied to the inverting terminal. The reference and feedback network sets the hysteresis window.

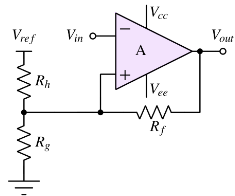
Threshold Voltages​

VTH=Vref(RgRh+Rg)+VOH(RhRh+Rg)V_{TH} = V_{ref}\left(\frac{R_g}{R_h + R_g}\right) + V_{OH}\left(\frac{R_h}{R_h + R_g}\right) VTL=Vref(RgRh+Rg)+VOL(RhRh+Rg)V_{TL} = V_{ref}\left(\frac{R_g}{R_h + R_g}\right) + V_{OL}\left(\frac{R_h}{R_h + R_g}\right)

Hysteresis Width​

ΔVH=VTH−VTL\Delta V_H = V_{TH} - V_{TL} ΔVH=(VOH−VOL)(RhRh+Rg)\Delta V_H = (V_{OH} - V_{OL})\left(\frac{R_h}{R_h + R_g}\right)

Resistor Ratio​

RhRh+Rg=ΔVHVOH−VOL\frac{R_h}{R_h + R_g} = \frac{\Delta V_H}{V_{OH} - V_{OL}}

Non-Inverting Comparator with Hysteresis​

note

The input signal is applied to the non-inverting terminal. Positive feedback shifts the reference voltage dynamically.

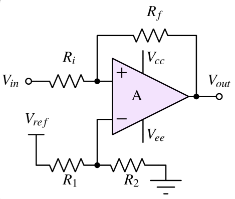
Threshold Voltages​

VTH=Vref+(R1R1+R2)VOHV_{TH} = V_{ref} + \left(\frac{R_1}{R_1 + R_2}\right)V_{OH} VTL=Vref+(R1R1+R2)VOLV_{TL} = V_{ref} + \left(\frac{R_1}{R_1 + R_2}\right)V_{OL}

Hysteresis Width​

ΔVH=(VOH−VOL)(R1R1+R2)\Delta V_H = (V_{OH} - V_{OL})\left(\frac{R_1}{R_1 + R_2}\right)

Resistor Ratio​

R1R1+R2=ΔVHVOH−VOL\frac{R_1}{R_1 + R_2} = \frac{\Delta V_H}{V_{OH} - V_{OL}}

Design Guidelines​

tip
  • VOHV_{OH} and VOLV_{OL} are the comparator output high and low saturation voltages
  • Choose resistor values between 10 kΩ and 1 MΩ
  • Higher resistance reduces power consumption but increases noise sensitivity

How Hysteresis Is Added​

By feeding a small portion of the output back to the input (positive feedback).

Result:

  • Clean transitions
  • Stable digital output
  • Perfect for MCU inputs

📌 A comparator without hysteresis is incomplete in real systems.

🌉 Signal Conditioning – Bridging Analog and Digital​

Microcontrollers don’t understand raw sensor signals well.

Signal conditioning prepares signals so the ADC or digital input can read them correctly.

🛠️ Problems Signal Conditioning Solves​

1️⃣ Tiny Signals​

Sensor: 0–10mV0–10mV

ADC wants: 0–5V0–5V

✅ Solution: Amplification

2️⃣ Noisy Signals​

Long wires, EMI, motors, switching supplies introduce noise.

✅ Solution: Filtering

3️⃣ Offset Signals​

Sensor:
2V→0 measurement2V \rightarrow 0 \text{ measurement} 3V→full scale3V \rightarrow \text{full scale}

ADC wants: 0–5V0–5V

✅ Solution: Offset removal + gain

4️⃣ Loading Problems​

Sensor has high output impedance → voltage droops.

✅ Solution: Buffering

🧱 Signal Conditioning Building Blocks​

Typical stages:​

  1. Amplification
  2. Filtering
  3. Level Shifting
  4. Buffering

📊 Simple Conditioning Example​

Pressure sensor: 0–100mV⇒0–10 bar0–100mV \Rightarrow 0–10\text{ bar}

Arduino ADC: 0–5V⇒0–10230–5V \Rightarrow 0–1023

Required gain:​

Av=5V100mV=50A_v = \frac{5V}{100mV} = 50

Result:​

  • 0–100–10 bar maps cleanly to 0–10230–1023 counts
  • Excellent resolution
  • Low noise

🎛️ Filtering – Removing Noise​

RC Low-Pass Filter​

  • Passes slow sensor changes
  • Blocks fast noise

Cutoff frequency:

fc=12πRCf_c = \frac{1}{2\pi RC}

Active Filters (Op-Amp Based)​

  • No loading
  • Precise cutoff
  • Gain + filtering together

Preferred for sensor interfaces.

🔀 Level Shifting – Matching Ranges​

Example 1: Bipolar to Unipolar​

Sensor: −5V→+5V-5V \rightarrow +5V

ADC: 0–5V0–5V

Solution:

  • Gain = 0.50.5
  • Offset = +2.5V+2.5V

Result: −5V→0V,0V→+5V-5V \rightarrow 0V,\quad 0V \rightarrow +5V

Example 2: Low Voltage Sensor​

Sensor: 0–1V0–1V

ADC: 0–5V0–5V

Solution: Av=5A_v = 5

🔒 Buffering – Protecting Signals​

A voltage follower:

  • Gain = 1
  • Infinite input impedance
  • Very low output impedance

Why it matters​

  • Prevents ADC loading
  • Isolates sensor
  • Improves accuracy

🔗 Typical Signal Chain​

Sensor → Amplifier → Filter → Buffer → ADC → MCU

Each block is simple. Together, they make the system reliable.

🎯 Why This Matters for Beginners​

Most “random” issues are actually:

  • Noise
  • Poor impedance matching
  • Missing filtering
  • No hysteresis

Good signal conditioning turns: ❌ flaky circuits
✅ into rock-solid systems

✅ The Bottom Line​

  • Comparators turn analog values into decisions
  • Hysteresis makes decisions stable
  • Signal conditioning makes sensors usable
  • Op-amps make all of this cheap, simple, and reliable

Master these ideas, and you’re designing real-world electronics, not just lab demos.